1. Введение

 

Среди задач, обычно относимых к ИИ, можно выделить две основных категории: задачи автоматической выработки оптимального поведения и задачи автоматического построения моделей окружающей среды (то есть извлечения знаний из данных).

Мы будем говорить о втором типе задач. При этом будет предполагаться, что «окружающий мир» фактически дан решающему алгоритму как некий набор входных примеров (к примеру, набор показаний сенсоров в последовательные моменты времени), и задачей алгоритма является построение модели, адекватно описывающей этот набор.

Формализация слов “адекватно описывающей” встречает затруднения. Мы могли бы сказать, что модель адекватно описывает входной поток, если она позволяет делать верные заключения о будущих срезах потока (показаниях сенсоров в фиксированный момент времени), опираясь на значения предыдущих срезов. Однако, задача сколько-нибудь точного предсказания будущих срезов потока, видимо, неразрешима. Во всяком случае, человеческий интеллект ее не решает. Действительно, хотя мы, в принципе, можем представить себе, что мы будем видеть в следующие моменты времени, если совершим те или иные действия, но эта “картинка” вовсе не совпадет “попиксельно” с реальной. Больше того, если сравнить “предсказанные” значения среза с реальными, мы видим, что они не являются схожими в сколько-нибудь простой “метрике”.

Интереснее рассматривать модели, с помощью которых можно вычислить будущие срезы потока (или какие-то их отдельные характеристики), имея  на входе предыдущие срезы и некоторое количество произвольно выбираемых чисел (объектов), которые далее будем называть свободными параметрами. Мы далее будем называть “реализацией” множество моделей, которым оперирует строящий их алгоритм. Можно говорить, что построенная модель адекватно описывает поток, если она не встречает противоречащих ей фактов, то есть, если для каждого нового среза потока в данной модели мог быть получен (при задании должных свободных параметров) результат, “достаточно похожий” на наблюдаемый.

Условие отсутствия противоречий модели во входном потоке, судя по всему, является необходимым признаком адекватной модели, но не является достаточным. В самом деле, простейшей “моделью”, удовлетворяющей такому условию, будет модель “возможно все”, в которой неопределенность, создаваемая неизвестными параметрами, очень велика и позволяет согласовать модель не только с реальными срезами потока, но вообще с любыми наборами величин (другими словами, в этой простейшей модели исходные данные описываются, как совокупность отсчетов некоторой случайной величины). Поэтому естественно сформулировать дополнительное условие минимальности неопределенности, вносимой свободными параметрами модели. Это условие, по сути, является формализацией бритвы Оккама: “не следует вводить сущностей сверх необходимых”.

            Вообще, принцип бритвы Оккама неявно включен во все методы выбора модели. Для формальной реализации бритвы Оккама необходимо оценить “экономичность” модели по отношению к имеющимся данным. Поскольку выбор модели можно интерпретировать как построение описания наблюдательных данных, то в качестве такой оценки выбирается длина полученного описания. Таким образом, одним из общих принципов выбора модели для некоторого набора данных является принцип минимальной длины описания (МДО), который формулируется следующим образом: следует выбрать ту модель, которая позволяет описать данные наиболее коротко. Правила построения описания (и оценка его длины) и будут являться формализацией понятия “адекватности описания”.

            Прежде чем переходить к вопросам применения принципа МДО при выборе модели, вкратце рассмотрим понятие энтропии.

 

2. Энтропия

2.1. Энтропия дискретной случайной величины

 

Пусть нам дана дискретная случайная величина, которая может принимать N значений с вероятностями p₁, p₂, …, p_N. Тогда величина  (1) называется энтропией данной случайной величины.

Содержательный смысл энтропии такой: пусть мы кодируем каким-то двоичным кодом значения этой случайной величины. Назовем «буквой» двоичную последовательность, соответствующую одному значению. Не обязательно, чтобы «буквы» имели одну и ту же длину, но обязательно условие, что ни одна из двоичных последовательностей не должна начинаться с другой (тогда несколько «букв» можно передавать подряд без пауз, и эту последовательность все равно можно будет однозначно расшифровать).

Тогда верна такая теорема: средневзвешенная длина «буквы» всегда не меньше энтропии величины. То есть, если L_i – длина i-той «буквы», то сумма  не меньше Е.

Это означает, что если мы «передаем по телеграфу» (или, например, храним в памяти) N значений этой случайной величины (при этом i-тое значение встречается с вероятностью p_i), то каким бы совершенным ни был наш код, мы все равно потратим в среднем не меньше Е*N бит.

В то же время, эта оценка является достаточно точной. Во-первых, она достижима: существуют наборы p_i и коды для них такие, что . Во-вторых, для любого набора p_i  есть «достаточно хороший код», то есть такой, что энтропия и средняя длина «буквы» кода отличаются не больше, чем на 1.

 

2.2. Энтропия непрерывной случайной величины

 

Пусть задана непрерывная случайная величина с плотностью вероятности p. По аналогии с формулой (1) можно определить для нее величину  (2) Здесь интеграл определенный, берется по всему множеству значений величины.

            Очевидно, значения непрерывной случайной величины можно задавать с помощью дискретного кода только с некоторой точностью. Верно следующее утверждение: для задания значений с точностью до малого , требуется код со средней длиной (в том же смысле, что и в предыдущем абзаце) не менее чем .

Понятие энтропии случайной величины (и дискретной и непрерывной) имеет смысл не только при передаче ее значений при помощи двоичного кода. Чем энтропия больше, тем меньше вероятность того, что случайная величина постоянно принимает некое определенное значение. Чем энтропия случайной величины меньше, тем более уверенные предположения о том, каким окажется значение этой величины, мы можем делать еще до того, как оно стало известно.

 

2.3. Длина описания простейшей модели

 

Как отмечалось выше, простейшей моделью входных данных можно считать их интерпретацию в качестве отсчетов некоторой случайной величины. Таким образом, длина описания этой модели приближенно равна энтропии, умноженной на объем выборки. Следует отметить, что сформулированные теоремы о минимальной длине сообщения верны лишь для выборок из статистически независимых отсчетов данной случайной величины. Если это предположение неверно, то длина описания простейшей модели не будет являться минимально возможной, так что ее удобно использовать в качестве верхнего ограничения на длину описания. Теперь рассмотрим применение МДО принципа к выбору между содержательными моделями.

 

3. Классический подход

 

В этом разделе мы рассмотрим применение МДО подхода к задаче выбора модели на важном частном примере. Это рассмотрение позволит выявить основные принципы функционирования этого подхода, а также те сложности, которые могут возникнуть в более общих случаях.

 

3.1 Длина описания параметрической модели

 

Пусть дана обучающая выборка, состоящая из N векторов входов  и выходов , i=1..N. Поскольку любые измеренные величины всегда содержат некоторую ошибку, обычно бывает полезным разделять описание регулярной компоненты данных и описание остатков, образующихся после извлечения этой регулярной компоненты, представленной некоторой моделью, из данных. Рассмотрим случай аддитивной ошибки.

Итак, будем называть моделью функцию  (3), зависящую от входа Х и нескольких дополнительных параметров: регулярной части  и случайных прибавок (вектора ошибок) . Здесь  описывает функциональную зависимость между данными, а – ошибку описания.

Мы будем рассматривать только модели, согласованные с обучающей выборкой, то есть считать, что для любого i,     (4).

Каждый из параметров П (не только элементы вектора ошибок, но и регулярные параметры) удобно для дальнейшего рассмотрения представлять себе как некоторую случайную величину и задать ее распределение из тех или иных соображений. Например, можно считать, что вектор ошибок распределен нормально, и оценить параметры нормального распределения, исходя из известных нам ошибок .

            Тогда математическое ожидание (точнее, его оценка, полученная путем усреднения по обучающей выборке) длины описания данной модели будет равно , где K - число параметров модели.

            В качестве примера можно рассмотреть простейшую модель, в которой функциональная зависимость отсутствует. То есть , где П - случайная величина. Значит, длина описания такой модели будет равна объему выборки, умноженному на энтропию Y.

Рассмотрим некоторые возможные случаи на примере задачи аппроксимации набора точек многочленом произвольной степени.

 

3.2. Выбор модели

 

            Пусть дано N пар {X_i,Y_i}. И пусть требуется построить полином p(X,П₁), наиболее хорошо описывающий данную совокупность точек. Исходя из условия (3) можно записать: П_2i = Y_i - p(X_i,П₁), i=1..N. П₁ – совокупность коэффициентов при соответствующих одночленах и их степени. Согласно принципу минимальной длины описания, требуется решить задачу:

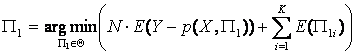           (5).

Здесь  - множество возможных значений параметров.

 

3.2.1. Случай постоянной длины описания регулярной компоненты

            Рассмотрим частный случай. Пусть . То есть, мы рассматриваем ситуацию, при которой длина описания полинома не зависит от значений его коэффициентов (например, мы рассматриваем полиномы только фиксированной степени, отводя на каждый коэффициент определенное число байт). В этом случае для сравнения длин описания двух моделей следует лишь сравнивать энтропию остатков E(Y - p(X,П₁)). Можно показать, что тогда минимум энтропии совпадает с минимумом величины среднеквадратичного отклонения RMS(Y - p(X,П₁)) в том случае, если остатки – это случайные величины, распределенные по Гауссу (см. рис. 1). Поэтому критерий минимальной длины описания актуален тогда, когда распределение не является нормальным и если следует сравнивать модели различной степени сложности. В противном случае, критерий минимальной длины описания совпадает с критерием, применяемым в методах наименьших квадратов, однако, является более сложным для вычисления (из-за необходимости нахождения эмпирической оценки энтропии).

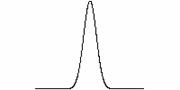
Рассмотрим случай, когда ошибки распределены не по Гауссу. Тогда результаты при использовании этих двух критериев могут быть существенно различными (см. рис. 2). Однако на этом примере не видно преимущество критерия описания минимальной длины. Для того чтобы продемонстрировать это преимущество, обратимся к несколько другой задаче.

	Рис. 1. Пример совпадения результатов выбора модели по критерию наименьших квадратов и по эмпирической энтропии в случае гауссового распределения ошибок (справа).

 

 

 

 

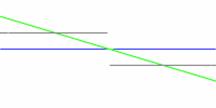
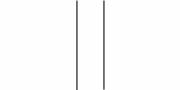
Рис. 2. Различие результатов выбора модели по критерию наименьших квадратов (зеленый) и по эмпирической энтропии (синий); функции распределения остатков после выбора модели для E-критерия (посередине) и для rms-критерия (справа).

 

 

 

 

Пусть есть два набора регулярно расположенных точек. Требуется определить смещение, которое приводит эти наборы в соответствие (см. рис. 3). В данном случае искомая модель имеет один параметр – смещение. Оптимальное смещение можно находить, рассматривая коэффициент корреляции (или среднеквадратичное отклонение). Однако, как видно из рисунка, в случае, если функции преобразованы друг относительно друга нелинейно, то минимум среднеквадратичного отклонения не соответствует правильному смещению. Применим принцип минимальной длины описания к данному случаю. Поскольку рассматривается простейшая модель (лишь смещение), то исходные данные представляются в виде случайной величины. Предполагая конкретное относительное смещение двух наборов данных, получаем одну векторную случайную величину , плотность распределения которой зависит от смещения . Энтропия этой случайной величины равна совместной энтропии величин  и : , где  - плотность вероятности совместного появления  и . Как видно из графика, совместная энтропия имеет минимум при верном смещении, не смотря на нелинейное преобразование между двух наборов исходных данных. Таким образом, в ряде задач преимущество использования критерия минимальной длины описания очевидно.

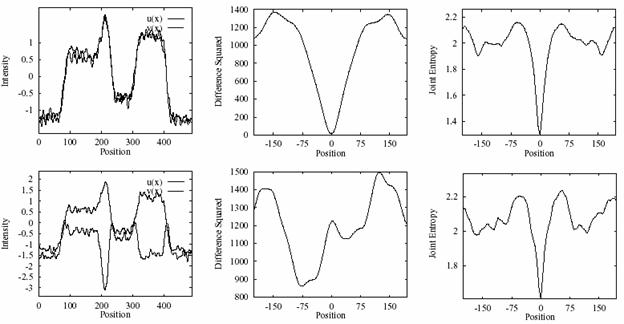
Рис. 3. Сравнение МДО и RMS критериев в задаче совмещение двух наборов данных. Слева: совмещенные наборы в случае их совпадения с точностью до аддитивной гауссовой ошибки (сверху) и нелинейно преобразованные относительно друг друга (снизу). Посередине: зависимость значения RMS от смещения, справа: зависимость совместной энтропии от смещения.

 

 

 

 

 

3.2.2. Выбор между разнородными моделями

 

Другое применение этого критерия, как уже отмечалось, возможно в том случае, если присутствует выбор между моделями разной степени сложности. Во всех известных авторам реализациях (множествах моделей) существует одна и та же дилемма: чем больше количество параметров в модели, тем она точнее описывает совокупность данных, но тем ниже надежды на то, что такая модель окажется адекватной. При уменьшении же числа параметров модели, уменьшается и ее практическая значимость, поскольку такая модель гораздо менее точно описывает данные. В частности, такая же проблема возникает и при разработке нейронных сетей, как проблема переобучения (при сильной специализации нейронная сеть теряет способность к обобщению).

В рамках МДО принципа данная проблема весьма изящно разрешается. Для примера, вернемся к задаче описания набора точек полиномом произвольной степени (см. уравнение 5). Общая модель разделена на две составляющие: регулярная часть (описание многочлена П₁) и случайная часть (описание остатков П₂). Длина описания случайной компоненты может уменьшаться за счет добавления новых членов в полином, но при этом увеличивается длина описания регулярной составляющей модели. В общем случае можно построить полином, точно описывающий данный набор точек. Но для этого потребуется число параметров, равное числу точек, а значит, длина описания такой модели будет примерно соответствовать длине описания исходных данных с помощью простейшей модели. То есть, два крайних случая (описание наблюдений как совокупности отсчетов случайной величины и с помощью только регулярной составляющей за счет использования числа параметров, равного числу точек) приблизительно одинаково плохи.

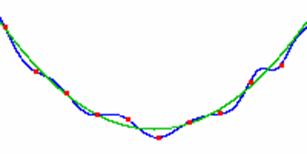
Рис. 4. В данном примере описание набора из 9 точек кривой второго порядка оказывается более оптимальным в контексте принципа описания минимальной длины, чем точное описание этих точек кривой 8-го порядка

 

 

 

К сожалению, на практике оценка обоих слагаемых в уравнении (5) может являться весьма нетривиальной задачей. Для надежной эмпирической оценки энтропии (особенно вещественных случайных величин, для которых возникает также проблема выбора шага дискретизации) требуются достаточно объемные выборки. А для определения длины описания регулярной составляющей, для которой требуется оценка энтропии коэффициентов П₁ (которые также рассматриваются как случайные величины), зачастую требуются априорные знания плотностей вероятности. Рассмотрим, например, такой случай. Пусть у нас есть три точки. Их можно точно описать параболой или синусоидой. Если мы априорно знаем, что это парабола, то нам потребуется лишь 3 числа. То же самое и с синусоидой. Но если допустим и тот и другой вариант, то в модель нужно вносить дополнительную информацию. Какое из описаний при этом будет короче? Ответ на этот вопрос зависит от выбора “языка” описания модели. То есть, этот “язык” и устанавливает неявно априорные вероятности появления моделей.

Таким образом, хотя количества информации для регулярной и случайной компонент имеют один и тот же “физический смысл” (энтропия случайной величины, умноженная на объем выборки), способы их оценки сильно различаются, поэтому на практике при сложении оценок этих двух длин описания можно вводить между ними некий коэффициент пропорциональности, который определяется на основе некоторых эвристических соображений и уточняется эмпирически. И тем не менее, в каждом конкретном случае эту проблему можно решить. Что позволяет решать проблемы типа переобучения, а также производить “тонкую настройку” методов выбора модели.

 

4. Обобщенный подход

4.1 Отличия от классического подхода

 

Как было отмечено в предыдущей части работы, основной сложностью при выборе модели является совместная оценка длин случайной и регулярной компонент. В конкретных практических случаях эту проблему удается решить эмпирически, что не удовлетворительно с точки зрения теории. В этой части работы мы рассмотрим общий подход, позволяющий распространить принцип минимальной длины описания на более широкий класс моделей по сравнению с моделями вида (3).

Во-первых, случайную составляющую мы уже не будем считать просто «прибавкой». Случайные и неизвестные факторы будут являться равноправными параметрами функции. Приведем простейший пример модели, которая не укладывается в формулу (3):

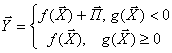. Здесь g(X) можно представлять себе как некий «критерий безошибочности». П – случайная составляющая, которая действует при определенных «условиях возникновения ошибки».

Такое обобщение связано с тем, что часто бывает полезно рассматривать модели, в которых случайные факторы влияют по-разному в зависимости от известной части входа: в некоторых условиях модель дает более уверенную оценку для Y, в некоторых – менее.

Во-вторых, мы обобщим и вид регулярной составляющей. В предыдущей части доклада рассматривались модели с регулярными частями только вида . То есть, регулярная составляющая полностью задавалась фиксированным числом параметров. Сейчас мы будем говорить о моделях, которые представляют собой произвольную функцию, выбранную из множества возможных («реализации»). При этом «реализация» может быть множеством многочленов заданной степени (такой пример укладывается в рамки рассмотренного ранее частного случая), а может быть и множеством машин Тьюринга (а такой уже нет).

Поскольку общность становится существенно выше, в данном подходе становится сложно сформулировать принцип минимальной длины, и нам придется разделить понятие «длина описания» на две части.

Одна из них – «неопределенность модели», вносимая свободным параметрами, является обобщением понятия «длина описания вектора ошибок». Если случайные параметры действуют простейшим образом, как прибавки (как это рассматривалось в предыдущем разделе), то неопределенность и будет совпадать с «длиной описания вектора ошибок». Новая величина будет введена именно для того, чтобы уметь корректно посчитать неопределенность в тех случаях, когда случайные параметры действуют как-то иначе. Неопределенность можно вычислить для модели, представленной любой измеримой функцией. Понятие «неопределенность модели» зависит только от самой модели, но не зависит от того, из какой реализации модель взята.

Вторая часть - длина описания регулярной части, напротив, полностью зависит от реализации, и не зависит от распределения случайных параметров.

Почти весь дальнейший текст посвящен тому, как учесть две этих разных величины в рамках одного и того же критерия. Для этого нашелся довольно изящный способ - «признак неулучшаемой модели».

4.2. Степень неопределенности модели

 

            При заданном входе Х значение выхода модели в зависимости от свободных параметров представляет собой случайную величину, заданную на декартовом произведении тех вероятностных пространств, на которых заданы эти параметры. Это утверждение можно расшифровать следующим образом: если мы знаем, каково распределение параметров, и какова функциональная зависимость между значениями параметров и выходом модели при заданном входе, то мы можем вычислить и функцию распределения выхода (а значит, и любые зависящие от нее характеристики, например, вероятность, с которой выход принадлежит некоторому множеству).

            Энтропию этой случайной величины (выхода) мы будем называть степенью неопределенности модели при заданном входе. Если усреднить эту величину, вычисленную по всем входам обучающей выборки, мы получим степень неопределенности как таковую. Чем она меньше, тем более «сильной» является такая модель.

Первый пример. Степень неопределенности модели F(X, П) = f(X) + П, где П – «ошибка», равна энтропии случайной величины П (и не зависит от обучающей выборки).

Второй пример. Пусть модель выглядит следующим образом: , где g(X) – некий «критерий безошибочности». Тогда степень неопределенности модели равна энтропии случайной величины П, умноженной на относительное число тех примеров в обучающей выборке, для которых .

На практике, чем сложнее модель и ее связь со свободными параметрами, тем сложнее вычислить степень неопределенности. Впрочем, эта задача относительно проста, если функция F принимает только небольшое число значений. Тогда можно, взяв «наугад» достаточно много наборов параметров, приближенно вычислить вероятности, с которыми она принимает то или иное из своих возможных значений, после чего вычислить энтропию непосредственно. Если зависимость модели от свободных параметров достаточно проста, как в вышеприведенных примерах, то степень неопределенности легко вычисляется аналитически.

Понятие степени неопределенности модели весьма мощно. Оно позволяет сравнивать модели совершенно разной природы, с разным числом свободных параметров.

4.3. Основная дилемма

 

            В пункте 3.2.2 уже обсуждалась дилемма между информативностью и надежностью  модели: чем ниже степень неопределенности модели, тем ниже и надежды на то, что она окажется адекватной. В то же время чем выше степень неопределенности, тем меньше практическая значимость такой модели. В этом пункте мы еще раз рассмотрим ее с точки зрения более общего подхода.

Для снятия этой дилеммы в классическом подходе предлагается рассматривать сумму , где L – длина описания регулярной части модели, а Е – ее неопределенность. Считается, что наиболее «правильной» будет та модель, для которой достигается минимум этой суммы. Числовой коэффициент обычно полагают равным единице.

Этот же метод можно без каких-либо изменений предложить и в рассматриваемом теперь более общем случае. Однако нужно понимать, что «длина описания модели» и «степень неопределенности» - величины разной размерности. В связи с этим коэффициент  приобретает смысл коэффициента пересчета между двумя пониманиями «количества информации»: теоретико-вероятностным и содержательным. Проблема выбора коэффициента  весьма нетривиальна. Тем не менее, такой прием вполне применим на практике для достаточно простых реализаций.

4.4. Неулучшаемость модели

 

Можно предложить и другой, более обоснованный способ поиска «лучшей» модели, требующий, однако, больших усилий для понимания и применения.

Допустим, что в данной реализации можно ввести операцию «детализации модели», преобразующую модель неким стандартным образом, увеличивающим длину ее регулярной части и снижающим при этом ее неопределенность. Такая операция, разумеется, будет своей для разных реализаций. Для многих реализаций можно сформулировать несколько разных операций, действующих подобным образом.

К примеру, если реализация – множество компьютерных программ на некотором простом языке, в качестве операции «детализации модели» мы можем рассмотреть такую операцию над программой:

1.      Параметр П_i везде в тексте заменяется на переменную p_i

2.      В начало программы вставляется фрагмент вида «если вход совпадает с первым примером обучающей выборки, то p_i присвоить значение …, если вход совпадает со вторым примером, то p_i присвоить значение …»  и т.п.

В приведенном примере из исходной модели получится модель, в которой на один свободный параметр меньше. Можно показать, что ее степень неопределенности всегда окажется ниже, чем у исходной.

В общем случае результатом операции «детализации модели»  является другая модель, про которую можно с уверенностью сказать, что она, во-первых, заведомо менее адекватна, чем исходная, и, во-вторых, ее степень неопределенности ниже. Мы будем считать, что с помощью операции «детализации модели» можно автоматически получать модели сколь угодно маленькой неопределенности, вплоть до нулевой, которые при этом будут оставаться согласованными с обучающей выборкой.

Скажем, что модель М является «неулучшаемой», если длина описания любой другой известной нам модели, имеющей меньшую степень неопределенности, как минимум равна длине описания некоторой «детализации» этой модели (или больше нее), имеющей ту же (или меньшую) степень неопределенности. Иначе говоря, из М можно абсолютно «механически» получать модели, которые по обоим параметрам будут не хуже других известных нам моделей.

Представляется верным, что именно неулучшаемость модели является признаком ее адекватности и применимости одновременно. Естественно, чем лучше мы подберем операции «детализации модели», тем больше вероятность того, что какая-то из известных нам моделей окажется неулучшаемой.

Однако, для применения этого определения нужны значительные усилия: необходимо сформулировать операции детализации в данной модели, найти достаточно много моделей, согласованных с исходной выборкой, вычислить степени неопределенности каждой из них, применять операции детализации к «подозреваемым на адекватность» моделям и т.п.

4.5. Принцип минимальности в задачах извлечения знаний

 

Иногда рассматривается вариант задачи извлечения знаний из данных, в котором цель ставится иначе. Алгоритм в этой постановке должен формулировать «законы», описывающие входной поток. Каждый такой закон представляет собой некоторое соотношение, не являющееся тождеством, но выполняющееся на всех известных входах модели. При использовании найденного правила на практике, видимо, будет предполагаться, что оно будет выполняться и на будущих входах модели.

Рассматривая такую постановку задачи, мы будем называть реализацией множество всех возможных правил (законов).

Пусть правило формулируется в виде F(X)=C, где Х – вход, С – некоторая константа. Если мы каким-то естественным образом введем на множестве возможных входов структуру вероятностного пространства, мы сможем рассмотреть функцию F как случайную величину на этом пространстве. В этом случае энтропию F можно назвать информативностью правила. Конечно, можно называть информативностью и более простую величину: вероятность того, что F(X)=C. Часто так и поступают.  В любом из двух определений, чем выше информативность правила, тем это правило более применимо.

Как и в случае моделей, возникает дилемма: увеличивая длину описания правила, можно, с одной стороны, увеличивать информативность правила, с другой стороны, увеличивается и шанс «переобучения», то есть того, что в будущем это правило перестанет выполняться.

Для преодоления этой дилеммы можно пытаться максимизировать, например, отношение информативности правила к его длине. Можно сформулировать и признак «минимальности» правила, рассмотрев операцию «детализации правила». Достаточно понятно, как это можно сделать по аналогии с определением минимальности модели. Мы не будем на этом останавливаться.

5. Обучающая и тестовая выборки

 

Еще одна полезная стратегия проверки извлеченных знаний не относится к теме условий минимальности, но не упомянуть о ней нельзя. Это разделение примеров на «обучающую» и «тестовую» выборку с целью проверки адекватности правила или модели. Правило (или модель) находятся с использованием примеров только из обучающей выборки, после чего проверяется на соответствие на тестовой выборке. Если модель адекватна, соответствие будет достигнуто, в противном случае не будет (точнее, вероятность этого стремится к нулю с увеличением тестовой выборки). Такая техника хорошо известна при применении нейронных сетей, но ее можно использовать далеко не только там.

В случае задачи генерации правил, ее можно соединить с техникой оценки длины описания. Для этого нужно оценивать среднее число отвергнутых и принятых правил в зависимости от сложности правила. С увеличением сложности правила число последних будет стремиться к нулю, и можно найти некий порог сложности, после которого шанс найденного правила быть адекватным окажется незначительным. Этот порог можно будет считать верхним пределом сложности адекватного правила. Конечно, найденное пороговое значение сложности будет экспериментально подтвержденным только при данном количестве обучающих примеров, при данной структуре входного потока, и в данной реализации!

 

6. Иерархические модели

 

            Вернемся к понятию простейшей модели: F(X,П)=П. По сути, когда мы рассматриваем некоторую более сложную модель F(X,П), то параметры П этой модели можно рассматривать, как новые исходные данные, для которых выбирается простейшая модель. Здесь возникает идея построения иерархических моделей, а именно, для найденных параметров П строить собственную модель, отличную от тривиальной, и так далее.

Случайная составляющая (свободные параметры) не обязательно является шумом. Это могут быть и некоторые “неинформативные” параметры (то есть, параметры, не требующиеся системе для дальнейшего функционирования). В этом смысле, модель – это такое описание входных данных, которое инвариантно к свободным параметрам. Грубая аналогия: когда человек читает текст с экрана компьютера, он различает, каким шрифтом этот текст написан, но это информация ему не нужно для понимания содержания.

            Дальнейшее построение модели может производиться уже только для совокупности величин, определяющих регулярную часть модели. При построении модели происходит выявление релевантной информации и сокращение размерности исходных данных, что важно именно в “сложных” задачах.

            К такой задаче следует отнести в первую очередь проблему выявления знаний. Именно здесь построение иерархических моделей является наиболее актуальным. Длину описания нескольких правил (моделей) чаще всего можно сделать строго меньше суммы длин их описаний за счет выделения общих элементов в отдельные понятия. Поэтому заложенное в архитектуре самообучающейся системы стремление к минимальной длине описания поощряет появление в ней иерархии понятий. Очевидно, такая иерархия существует и у человека. Причем, эта иерархия прослеживается, начиная с первичной сенсорной информации и заканчивая сложной системой знаний. Существуют свидетельства, что человеческий мозг работает, исходя из МДО принципа. И действительно, если считать человеческий мозг в некотором смысле оптимальной информационной системой, то для наиболее рационального использования своих возможностей (как по объему памяти, так и по быстродействию) информация должна храниться в наиболее компактной форме. По крайней мере, можно считать установленным соблюдение этого принципа для начальных слоев зрительной системы человека.

            МДО подход к иерархическим системам также очень интересен с точки зрения установления связей между отдельными уровнями этой системы посредством общей целевой функции. Например, рассмотрим двухуровневую систему. Пусть мы решаем задачу построения модели сначала для первого уровня, а затем строим метамодель для некоторых параметров модели предыдущего уровня, рассматривая их как новые “наблюдения”. Такое последовательное построение моделей, очевидно, не даст общей оптимальной длины описания. В реальных задачах построение модели верхнего уровня дает возможность оптимизировать решение нижнего уровня, что является эффективным способом устранения ошибок и борьбы с шумами. В человеческом мозгу это осуществляется за счет эффекта адаптивного резонанса. Таким образом, адаптивный резонанс может также рассматриваться в рамках МДО подхода. Однако обсуждение этого механизма выходит за рамки данного доклада.