МЕТОД НАПРАВЛЕННОЙ ЭВОЛЮЦИИ

 

ИСХОДНЫЕ ДАНЫЕ И ПОНЯТИЯ

 

 

·        S – множество допустимых решений образующих пространство поиска

·        R – множество всех рациональных чисел

·        F(x) – функция оптимальности решения. xÎS, F:SÞR

·        M(x) – оператор мутации. Оператор мутации путем случайной модификации базового решения xÎS порождает новое решение. M:SÞS.

·        P – популяция решений

·        DIM(P) – объем популяции P

·        P₀ – стартовая популяция и P₀¹Æ

·        limit – максимальный допустимый размер популяции

·        PAR(x) – решение, в ходе мутации которого было порождено решение xÎS. PAR:SÞS.

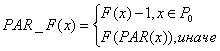·        , где xÎS

·        dF(x) = F(x) – PAR_F(x) , где xÎS. dF:SÞR

·        BEST(P) – функция возвращающая решение xÎP, где PÍS и P¹Æ, при котором значение F(x) больше либо равно чем при любом другом yÎP.

·        ROUND(x) – функция округления, где xÎR.

 

АЛГОРИТМ

 

1.      k := 0

2.      b := BEST(P₀)

3.      L := SUM{dF(x) | xÎP_k}

4.      P_k+1 := Æ

5.      для всех xÎP_k выполнять

5.1.   i := ROUND((dF(x) / L) * limit)

5.2.   если i = 0 то GOTO 6

5.3.   mutant := M(x)

5.4.   если F(mutant) > F(x) то P_k+1 := P_k+1 È {mutant}

5.5.   i := i –1

5.6.   GOTO 5.2

6.      если DIM(P_k+1) > 0 то

6.1.   new_b := BEST(P_k+1)

6.2.   если F(new_b) > F(b) то b := new_b

7.      если DIM(P_k+1) = 0 то

7.1.   result := b

7.2.   СТОП

8.      k := k +1

9.      GOTO 3

 

КОММЕНТАРИИ АВТОРА

 

1.      Результат работы алгоритма хранится в переменной result.

2.      Представленная схема алгоритма показывает общую логику и не направлена на оптимизацию вычислений. В частности, в ходе вычислений множество P_k при переходе на шаг 6 можно удалять из памяти.

3.      Пункт 5 позволяет подвергать мутации каждый xÎP_k в параллельном режиме.

4.      Как видно из алгоритма, преимущественное право на мутацию имеет не то решение, оптимальность которого выше (в традиционных эволюционных методах это приводит к преждевременной сходимости решения в точке локального оптимума), а то которое максимально превзошло родительское решение по оптимальности. Такая стратегия, с одной стороны  позволяет сохранить направленность перебора решений (по аналогии с градиентной оптимизацией) и в то же время  пытаться модифицировать только те решения, которые наиболее легко улучшить, а не те которые самые оптимальные. Если какое то направление поиска зашло в тупик, то запоминается ее лучшее достижение и вычислительные ресурсы перебрасываются на более перспективное направление поиска.

 

ОБСУЖДЕНИЕ

А. Плахов

Генетический алгоритм интересный, но, мне кажется, все еще не очень хорошо спасает от попаданий в «локальные ямы». Только это попадание возникает по другой причине, нежели в традиционном ГП. Недостаток, как мне видится, в том, что в каждое новое поколение добавляются только особи, которые оказались строго лучше предков. Возможно, стоило бы включить возможность добавления в популяцию и особей, которые хуже своего предка (с небольшой вероятностью), и изменить в пунктах 3 и 5.1 изменение dF(x) на (dF(x) + …), чтобы такие особи тоже могли «немножко размножаться».

 

Supremum

А это мысль. Что если пойти дальше и вообще оставлять все особи? По моему так будет намного лучше и исчезнет вопрос о выборе вероятности. Будут присутствовать как процессы эволюции, так и процессы инволюции(деградации). Как только эволюционная ветвь зайдет в тупик, для нее начнет преобладать процесс инволюции который позволит выйти из тупика.